garethmetcalfe Maths ideas

The New Deconstructing Word Questions – Y6

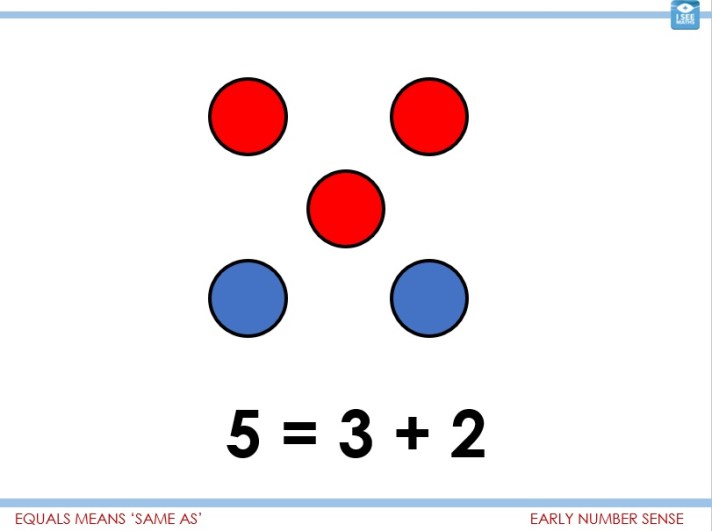
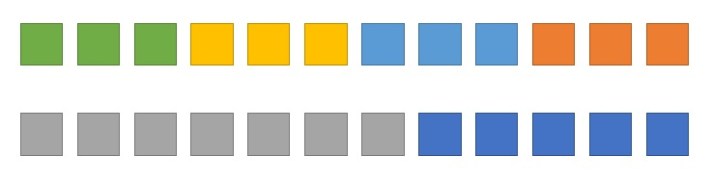
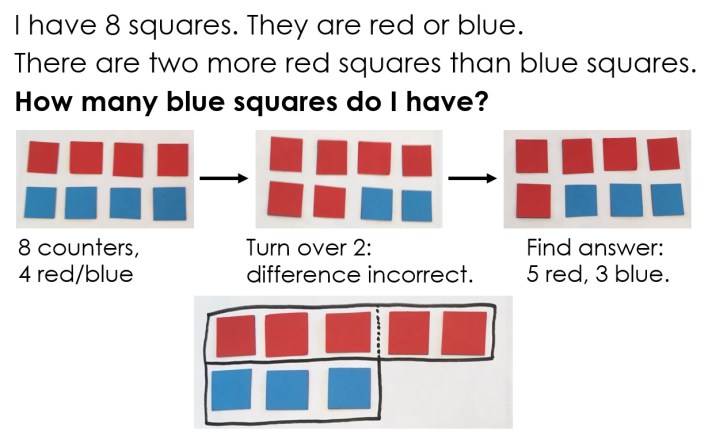
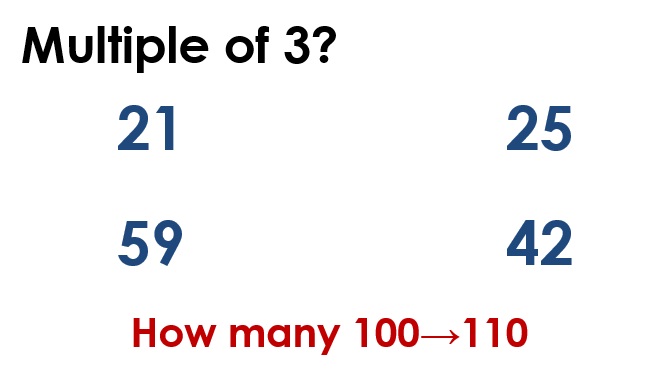The updated version of Deconstructing Word Questions – Y6 is now completed! Full information about the resource, including a free sample task, can be found here. It provides a coherent, detailed approach to teaching children to answer word questions and gives a wide range of thought-provoking challenges.

This resource has been re-released in April 2025. If you purchased the original resource, you can have this new version for free! Just email iseemaths@hotmail.com and attach the original version of the resource (as proof of purchase) or give the order number for your original order. Then, we will reply by sending you the new resource.

Why has the resource been updated and re-released?
Since writing the original version, I have written Deconstructing Word Questions resources for Year 2, Year 3, Year 4 and Year 5. All of these resources followed a specific lesson structure:
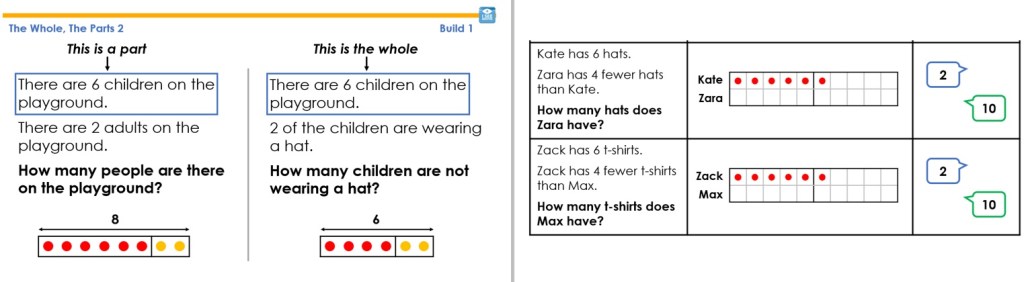
Build 1 – teaching prompts
Task A – pair discussion task
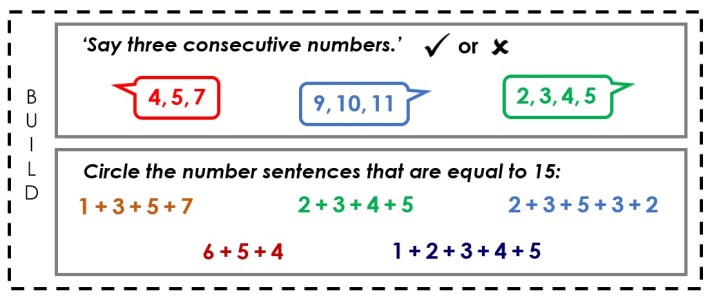
Build 2 – teaching prompts
Task B (Version 1 and 2) – questions
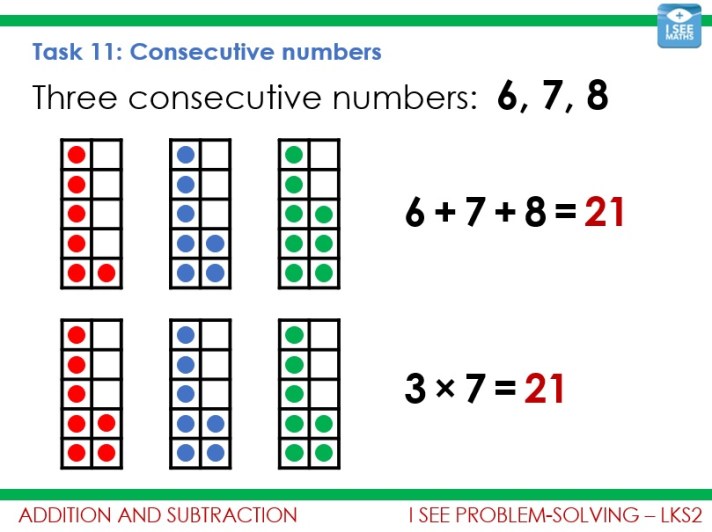
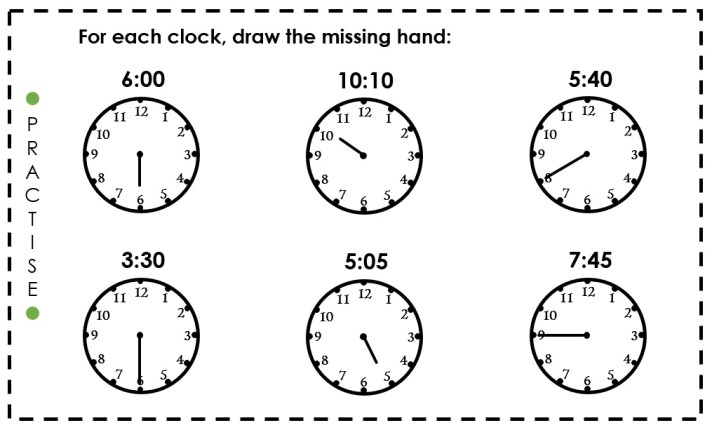
Extend – deeper challenge
I have re-written the year 6 resource so that it also follows this lesson structure. This means that the resources give a totally consistent whole-school approach to teaching children to answer word questions. This video shows how the resources can be used to teach a lesson:

I want schools to have a whole-school vision for teaching children to answer multi-step word questions. Therefore, I am running 90-minute online INSET sessions on 1st and 2nd September to communicate this vision. It would be great to have you involved!

The ability to answer word questions is one part of how we can build children as mathematical problem-solvers. The full vision, including detailed guidance and video exemplification, can be found on this page. I believe it gives a practical, exciting vision for how we can build all children as mathematical problem-solvers!

garethmetcalfe Maths discussion

Deconstructing Word Questions: the vision

Imagine this: you are asked to describe the strengths that the children in your school have as mathematicians. You say ‘they are brilliant at understanding and answering word questions!’ When asked to elaborate, you say ‘the children read questions carefully and pick out the important information.’ Or perhaps ‘the children are great at spotting multi-step questions.’ Maybe even ‘they show their understanding in different ways.’

In reality, so many children struggle to answer multi-step or non-standard word questions. So how do we go from giving children word questions to teaching all children to answer word questions? What does a consistent approach look like?

This has become my mission. For the last 3 years, I have been writing Deconstructing Word Questions for Y2 – Y6. Each task has been trialled in a number of different schools, being honed with the help of some amazing teachers. The eBooks are on sale here.

The golden thread that runs through every technique, every activity, is focusing children’s thinking on the deep structure of each question. It is about taking the attention away from calculating answers to understanding the steps involved. Here are four ways that this is achieved.

1. Slowly revealing information in questions
Children predict what the hidden words/information could be, as in the examples below (Y2 and Y5). Then, the information is revealed. This means children have thought about the structure of the question before they answer the question.

2. Using equipment or bar models
Sometimes, children are asked to represent questions with counters. Sometimes, children are asked ‘which bar model represents the question?’ (left-side example, Y3). For some questions, children are given part-complete bar models to fill which act as a scaffold (right-side example, Y4).


3. ‘Minimally different’ questions
Children analyse pairs of questions that are very subtly different. The children look at how the questions are the same/different. This helps children notice the subtle but all-important differences in the wording of questions (left-hand example, Y2). This variation is used in the questions that children answer (right example, Y3).


4. Depth
Lots of techniques are used to extend children’s thinking. This includes explaining which approach is correct (left example, Y2) or in giving the information that is missing in a question (right example, Y4).


There is a trial task for each year group to try out. Click on the links below for the resources and for the short ‘how to’ video:
Deconstructing Word Questions – Y2
Deconstructing Word Questions – Y3
Deconstructing Word Questions – Y4
Deconstructing Word Questions – Y5
Deconstructing Word Questions – Y6

The Vision: Building Problem-Solvers maps out a holistic vision for building children as problem-solvers. There are 10 videos to exemplify the key principles shared.

I hope Deconstructing Word Questions helps many children to grow as mathematical problem-solvers.

garethmetcalfe Uncategorized

UPDATED BLOG: My 2023-2024 Writing Challenge

I have managed to post an example task for a streak of 107 days this academic year. However, at this point I’m going to redirect my efforts as I have decided to focus on writing Deconstructing Word Questions Y2-Y5. I see this as being my greatest possible contribution. It’s hard to properly communicate the vision for these resource using photos – it’s better done using short videos. I will spend the Spring term focusing on writing the resources and trialling them in lots of different classrooms. Then, in the summer term, I will post a video a week explaining how, I believe, we can transform the teaching of word questions. I will also send out lots of free resources to trial to the people on my mailing list. I am so excited about what is to come!

The resources will be released some time between September 2024 and January 2025, depending on the outcomes from the classroom trials.

Below is my original blog post:

Day 1: The Mountain Pass Logic Puzzle and The Mountain Pass Answers

I’m passionate that all children get to experience the true richness of mathematics and for maths to be an intellectually and emotionally rich pursuit. To this end, over the last 10 years I’ve strived to create maths tasks that generate conversations, give space for curiosity and provide opportunities for extended exploration. I hope that my resources are inspirational and simple to integrate with your maths curriculum.

I have so many plans for new resources! I See Reasoning – Y1 and I See Reasoning – Y2 are being written: they will be comprehensive resources for building number sense and embedding reasoning in daily lessons. Deconstructing Word Questions will be written for Y1-Y5 after the successful launch of the Y6 eBook. Then I will go back to my roots: writing a range of logic puzzles and problem-solving ‘task families’, so problem-solving skills can be built coherently.

To get into the routine of writing new resources every day, I have set myself a challenge: to post a new task every school day on social media for the whole of the 2023-2024 academic year. Images or videos will be posted at 7:30pm every day on Twitter, Facebook and on my NEW INSTAGRAM FEED. At the time of writing, I have exactly 0 Instagram followers!

I am actively seeking your feedback on all my posts. Specifically, what would you change about each task? Or if you use any of the tasks in the classroom, what age of children did you use the task with and what happened? I won’t always respond immediately – I can struggle with insomnia so I’m usually off social media after 8pm – but I will read every comment. Feedback can be emailed to iseemaths@hotmail.com

I have taken so much from the feedback given by teachers about my work – it helps me to reject my bad ideas and improve my half-baked ones! I love to receive any suggested improvements or comments.

The first post will be on 4th September. Until then, have a great summer – Gareth

garethmetcalfe Maths ideas

I See Problem-Solving – LKS2: Support and Challenge

I’m delighted to have released I See Problem-Solving – LKS2. It’s a resource that I’ve lived and breathed in the classroom over the last 10 months! The aim is to help all children to access rich problem-solving tasks, whilst ensuring that all children are challenged and engaged. It is the practical outworking of the research on solving problems from this EEF report (see point 3). 

I See Problem-Solving – LKS2 is comprised of 54 tasks. Each task gives various challenges: the Build prompt introduces the key themes and concepts, before the main Task is presented. Then, there is a Support prompt to help children access the task. The Explain and Extend challenges give rich opportunities for extended exploration.  Here’s an example task, starting from the Build prompt:

This introduces some of the key language that the children will need to understand before they access the main task. Here is the Task:

Children might choose 1, 2 and 3; they could work with 21, 22 and 23. Either way, we can all explore this idea and visual representations can be used to help. If children are need help, they can look at the Support prompt:

The Worked Example shows the solution to the main task step-by-step. The Worked Example can be viewed as a PowerPoint or as a PDF:

To deepen the challenge, the Explain and Extend prompts provide related challenges:

Not all the tasks follow this exact format. Sometimes there are Practise questions:

And there are always questions that extend the challenge:

Information about the resource, plus a link to the Etsy page to buy the resource, is found on the I See Problem-Solving – LKS2 page. There are 5 free example tasks to use too. It costs £24.98 and is available as a digital download of the PDF file. I hope you find this resource super-helpful for engaging children in meaningful problem-solving. It’s certainly given me many great classroom moments already!

 

garethmetcalfe Maths ideas

I See Problem-Solving for LKS2 and KS1 – update 1!

After completing I See Problem-Solving – UKS2, I spent some time before Christmas extending my free resources for Early Number Sense and creating some free resources for visualising multiplication. Now it’s time for the next big project – writing I See Problem-Solving – LKS2 and I See Problem-Solving – KS1!

I’ve decided to write both resources simultaneously. Trialling the tasks takes so long, I thought was better to get going on both resources now. This will mean I can keep sending out sample resources to be trialled, keep making improvements to both and hopefully, overall, complete the I See Problem-Solving trilogy sooner! So far I have come up with loads of draft ideas for both resources in each curriculum area:

Soon I will start creating the tasks themselves. I’m going to start with tasks in addition and subtraction, multiplication and fractions. The idea is that the pre-task steps will help children to learn the sub-skills for answering the main task, making the activities accessible for all. Then there will be reasoning tasks and extensions for deepening learning. Expect lots of visual, thought-provoking mathematics!

Example tasks will be sent for trialling to people on my trial resources list for KS1 and LKS2: expect the first email mid-February. It helps so much when people tell me what they like about the sample tasks and what can be improved. I’m still very busy with my teaching and training commitments, so if I’m a bit delayed that’s why!

Once all the trialling is done, hopefully the finished product will help teachers to do something that I always found hard: systematically teach problem-solving skills to children. I’m mega-excited about what can be achieved.

I See Reasoning – KS1 and I See Reasoning – LKS2 are designed to help teachers build reasoning into daily maths lessons.

garethmetcalfe Maths ideas

Learning to Problem-Solve: number sequences and negative numbers

This is the first in a series of blog posts about how to systematically teach problem-solving skills using I See Problem-Solving, outworking the EEF research (recommendation 3) about using rich problems to learn mathematics.

Here’s the task that the class were given part-way through the lesson:

Before we get to this point, I want to break down the sub-steps involved in answering this question. First, a little pre-teach group are given this open task to bring back some prior learning:

Then we show the first part of the question that we are building up towards answering and these three example sequences. The children calculate (or spot) the first and then the second negative number in each sequence:

Now the children have a go at this short task. They identify that -4 is the second negative number in the first two sequences. I explain that, when writing the first two sequences, I actually started from -4 and added in equal steps, rather than starting from the positive number and subtracting (which would be more akin to trial and error):

Now the children are equipped to deal with the task. We work to find all the possible answers, noting that the sequence must decrease by more than 3 but less than 7. There ‘support’ prompt for children who need help, and some children also attempt the ‘explain’ or ‘extend’ tasks:

The free I See Problem-Solving Worked Example is used to show the three possible solutions. The following day, we pick up on a few misconceptions and look for ways to become more efficient, including looking at the example above and considering how we could add a multiple of 4 and 5 rather than the repeated adding.

I’m trying to make problem-solving accessible for all children, whilst ensuring that every child is challenged. I hope you find I See Problem-Solving super-helpful. The LKS2 and KS1 versions are in production!

Also in this series:
Equals Means Same As
Sum of the Digits Place Value Challenge

garethmetcalfe Maths ideas

Learning to Problem-Solve: sum of the digits

This is the second in a series of blog posts about how to systematically teach problem-solving skills using I See Problem-Solving, outworking the EEF research (recommendation 3) about using rich problems to learn mathematics.

When children have a really secure understanding of place value, I love using sum of the digit challenges. Here’s the task we’re coming to later:

The build-up focuses on the meaning of the sum of the digits. We start by ordering 74, 312, 214 & 47, and identifying how many digits in each number. Then we work out the sum of the digits for each, noting that the largest number, 312, had the smallest digit sum. To consolidate this skill, we have a go at this:

We also find numbers where the sum of the digits is 8. Example numbers that the children come up with include 53, 44000, 123500 and we even get an infinity sign for repeated zeros! Next, a quick recap on finding multiples:

After this, we are into the main task (number with sum of digits of 13, multiple of 4). Discussions were held about where to start: listing the multiples of 4, or finding all the 2-digit numbers with a sum of the digits of 13? The key question, it was decided was ‘which narrows down the possible answers more?’ Once the answer was found (76) it’s onto the explain and extend tasks:

 

We also made the point that, for the example above, we don’t need to cross out those beautiful workings out!

I’m trying to make problem-solving accessible for all children, whilst ensuring that every child is challenged. I hope you find I See Problem-Solving super-helpful. The LKS2 and KS1 versions are in production!

Also in this series:
Equals Means Same As Task
Number Sequences and Negative Numbers

garethmetcalfe Maths ideas

Learning to Problem-Solve: equals means same as

This is the third in a series of blog posts about how to systematically teach problem-solving skills using I See Problem-Solving, outworking the EEF research (recommendation 3) about using rich problems to learn mathematics.

I’m in Y5, building up to a task which requires children to understand the meaning of the =, < and > signs. To help model this idea, I show the children an image that they may have seen in KS1 from the Early Number Sense I See Maths page: at first the circles are white; then we see them coloured red and blue:

A range of other visual representations are used to show equivalence, including the image below to represent 4×3=7+5:

And this one to show 4×3>7+3:

Then the children write part-number sentences using different operations that are equal to 8, 10 and 12. They are positioned on the correct board. After that, children move the statements to make balancing number sentences, and sentences using the < & > signs:

Now we are ready for the main task. The support feature gives a clue: start by thinking about where to position the 8. Some children progress to the explain task, spotting different mistakes:

There is a super-challenging extend task that some children will get to tomorrow. We continue to model = as balance using scales and Numicon.

I’m trying to make problem-solving accessible for all children, whilst ensuring that every child is challenged. I hope you find I See Problem-Solving super-helpful. The LKS2 and KS1 versions are in production!

Also in this series:
Number Sequences and Negative Numbers
Sum of the Digits Place Value Challenge

garethmetcalfe Maths discussion

Counters & bar models used to unpick a classic PS question

This question is taken from the Y3 Autumn term White Rose Progress Check assessment:

I’ve really enjoyed exploring this question type (although, I have to admit, never yet with children as young as Y3). I want children to see and feel the structure of this type of problem, building up to being able to answer a question like the example above in small steps. Then, by working through a series of related questions, children will learn how to use efficient problem-solving strategies. They will also come to see that questions with different ‘surface features’ can have a very similar mathematical ‘deep structure’.

To start with, using double-sided red/blue counters, children attempt the question below:

Often, children start with 8 counters – 4 red, 4 blue. Then, they turn over two blue counters. They realise (with a nudge) that the difference between the number of red/blue counters is incorrect. With a bit more cajoling, we see only one counter needed turning over. At this point I line the counters up above/below each other. I suggest, rather than starting with the correct number of counters, we could start with the correct difference. Have 2 more red counters than blue counters; keep adding a red & blue until you have 8 counters.

That technique, or other methods, are then be practised using the question below. We note that this question is worded slightly differently, but see that the red/blue counters can still be useful:
This time, many children start by laying out four blue counters. We note that ten more counters are needed (5 blue, 5 red). Other children get 14 counters and experiment with how many to turn over. We look at these different approaches. Then, I draw a bar model around the counters (like for the original example), drawing a dotted line to highlight the difference of 4 counters.

Now it’s time for a worked example and another ‘different surface, same deep structure’ question. In this case, I model how to answer the question using the ‘start from the difference’ technique:
Having shown that the difference between the prices is 10p, the cost of the rubber can be calculated by halving 30p (a common incorrect answer to this question is pencil=30p, rubber=10p).

Children then attempt questions that have a very similar structure, still regularly using the counters. Some children are given slightly extended challenges:
Here’s another lesson example of how to break down the problem-solving process. I See Problem-Solving – UKS2 is designed to give teachers the tools to teach problem-solving systematically too. Work will start on the LKS2 version in January 2019. I can’t wait!

garethmetcalfe Maths ideas

Learning to Problem-Solve (and the role of I See Problem-Solving)

It’s easy to give children maths problems to solve; it’s much harder (and very time consuming) to systematically teach problem-solving so children become more competent problem-solvers. Here’s some thoughts on how my teaching of problem-solving has evolved and how I See Problem-Solving fits within this vision.

I have always loved engaging children in rich maths problems. The EEF research (recommendation 3) highlights the importance of engaging children in non-routine maths tasks. However, it also points out that such tasks can create a heavy a cognitive load for many children. Now I try I think more carefully about the sub-skills involved in solving a problem, and build up to the introduction of a problem-solving task using more carefully chosen examples. Consider this question:

Here’s how I built up to using this task. First of all, we clarify how to calculate the sum of four numbers and the difference between the smallest/largest numbers using this question:

Then we model the process of finding all possible answers with this prompt (answers: 5&5, 4&6, 7&3). We also highlight a likely mistake: 8&2 (the difference between the smallest/largest number no longer 4).

Then the final ‘pre-task’ question is introduced, focusing on the most difficult part of the calculation:

Now we get into the main task (sum of 4 numbers is 23, difference between smallest/largest = 4, all numbers different, how many ways?). Where appropriate, children use whiteboards and counters to access the task. When we find the answer 3, 4, 7, 9 we consider whether there is another solution that can be found keeping the 3&9 as the smallest/largest numbers.

As the lesson progresses, we explore systems for finding all possible answers and some children move on to the explain/extend tasks (which are variations on the main task). If you want to use Task 13, check out the free sample resources on this page. The solution to the problem is shown step-by-step by the pre-made worked example.

One little caveat: some children may benefit more from going straight into the question; others may need this extra scaffolding before getting into the main task. As ever, it’s about knowing your children.

There have been lots of great maths problems written. I hope that I See Problem-Solving takes things to the next level by presenting related problems and reasoning tasks in a coherent order, and by clearly representing the mathematics within the tasks.

I also hope that this blog gives food for thought about how to introduce problem-solving tasks so more children experience success. Enjoy using the resources!